The aim of this paper is to establish a link between quadrature surfaces (potential theoretic concept) and sandpile dynamics (Laplacian growth models). Given a measure $ \mu $ in $\mathbb{R}^d$ and a domain $\Omega$ containing the support of $\mu$, we call $\partial \Omega$ a quadrature surface for $\mu $ if one has $ \int_{\partial \Omega } h(x) d\mathcal{H}^{d-1} (x) = \int h(x) d\mu (x) $ for all functions $ h $ harmonic on $ \overline{\Omega} $ [Sh1] and [Sh2] by H. Shahgholian). For example, if $\mu$ is a Dirac mass concentrated at some point $x\in \mathbb{R}^d$, then a sphere with center at $x$ and of an appropriate radius would give a quadrature surface. There is no complete description of measures $\mu$ admitting a quadrature surface identity, but in a special case of a finite sum of Dirac masses, for instance, the existence is due to Shahgholian.

In this paper we show that one can obtain a quadrature surface as a scaling limit of a certain growth model on the lattice $\mathbb{Z}^d $, where $ d\geq 2 $. Our motivation comes from an already established connection between quadrature domains (these are domains admitting a similar integral identity as above, but with integration against the Lebesgue measure over the domain instead of the surface) and Laplacian growth models by Levine and Peres (see [LP1] and [LP2] ). They introduce a model called divisible sandpile, and prove that for initial distribution of finitely many points its scaling limit is a quadrature surface ( a smash sum of Euclidean balls, precisely, a concept after Diaconis and Fulton) A shift from a domain to a lower-dimensional object, a hypersurface in our case, seems to necessitate an entirely different approach.

To define our model, start with a distribution of mass $\mu_0 $ on $ \mathbb{Z}^d $, i.e. a bounded non-negative function of finite support, let $n = \sum_{x\in \mathbb{Z}^d} \mu_0(x) $ be its total mass, and fix a threshold $ m>0 $. One by one we pick a vertex $x \in \mathbb{Z}^d$ and if it carries mass larger than $m$, distribute the excess of mass from $m$ evenly among the $2d$ lattice neighbors of $x$. Otherwise, if the mass carried by $x$ is bounded by $m$ but the cumulative emissions of mass from $x$ prior to a given epoch of time exceed $\frac 1m n^{2/d}$ distribute the entire mass of $x$ evenly among its lattice neighbors. If none of the two conditions hold for $x$ we move on to another vertex. This mass redistribution procedure is called toppling of $x$. We show that provided any vertex of $\mathbb{Z}^d$ is chosen infinitely many times, the mass redistribution process will reach a stable state after countably many topplings, and regardless of the order of the topplings the final configuration will be the same (Abelian property). Informally, one may think about the proposed model, as a deformation of a divisible sandpile model of Levine and Peres, where we force the mass to accumulate on a $\frac 1m $-sub-level sets of the odometer. This model is partially inspired by singular perturbation problems in PDEs which are known to converge to Bernoulli type free boundaries.

The key concept in our analysis is the odometer function $u:\mathbb{Z}^d \rightarrow \mathbb{R}_+$ where for each $x\in \mathbb{Z}^d$ the value $u(x)$ shows total emissions of mass from $x$ during the lifetime of the process. In terms of this function, the discrete PDE problem solved by the model reads $$\Delta u(x) + \mu_0(x) \leq m \ \ \ \text{ everywhere on } \mathbb{Z}^d $$ and $$\Delta u(x) = m \mathbb{I}_{ \{ 0 < u < \frac{1}{m} n^{2/d} \} } (x) - \mu_0(x) \ \ \ \text{ for all } x \in \{u > 0\},$$ where $\Delta$ is the discrete (normalized) Laplacian. We show that the odometer $u$ is precisely the smallest super-solution to the above problem. This characterization combined with combinatorial moving plane techniques, which we introduced in our earlier paper, allows to get a certain discrete monotonicity properties for the odometer function for a single source initial distributions, using which we show that the set of visited sites of the model in $\mathbb{Z}^d$ grows proportional to $n^{1/d}$, and the entire mass of the system is being distributed to an annular ring of thickness $\sim 1/m$.

We prove the existence of the scaling limit of the model generated by a single source, and fixed threshold $m$. As we show, this limit is a ball, with the entire mass of the system being redistributed onto a narrow annular ring of thickness $\frac 1m$ near the boundary of the ball. With compactness arguments, we conclude that there is also a scaling limit for a subsequence of the odometers, if the threshold $m$ tends to infinity along with the scale of the model. That limit is spherical, with the entire mass of the system being uniformly redistributed onto the boundary of that ball. This gives a quadrature surface for a single source mass distributions.

We introduce a new lattice growth model, which we name boundary sandpile and which amounts to potential theoretic redistribution of the given continuous mass on the lattice $\mathbb{Z}^d$ onto the combinatorial (free) boundary of some unknown domain, which is being determined by the dynamics of the model.

Our initial motivation was triggered by an intriguing connection established by Levine and Peres, between quadrature domains, a potential theoretic concept, and divisible sandpile, a growth model on the lattice. In this paper we attempted to create a sandpile dynamics (a growth model on $\mathbb{Z}^d$) which would have a quadrature surface as its scaling limit. On the way to this quest, which is yet to be fulfilled, we introduce a new growth model, the boundary sandpile, which seems to represent a new alluring phenomenon not encountered previously.

To define boundary sandpile model, assume we have concentration of (continuous) mass $n > 0$ at the origin of $\mathbb{Z}^d$ $(d\geq 2)$. Then, at any discrete time $k\geq 0$, we say that a site $x\in \mathbb{Z}^d$ is visited, if at a certain time before (and including) $k$ it carried positive amount of mass. Next, at time $k$ we call a site $x$ unstable, if either $x$ is in the interior of the visited sites and has positive mass, or $x$ is on the (discrete) boundary of the set of visited sites, and has mass larger than $n^{1/d}$ (this threshold is due to scaling considerations). Then, any unstable site can topple, by evenly distributing all its mass among its neighboring vertices on the lattice. The process terminates, if there are no unstable sites. Clearly, this redistribution never stops in finite time, except for trivial cases, and it is not clear a priori, if the order in which one topples the unstable sites, can affect in any way the limiting growth cluster. What we showed in the paper, is that in the limit, i.e. as the discrete time goes to infinity, the growth process finds a stable configuration provided all unstable sites are toppled infinitely often; moreover, the limiting configuration is independent of the toppling sequence, and in this sense the model is abelian. By definition, the total mass of the system is being redistributed to a combinatorial free boundary determined by the underlying dynamical system. Some limiting shapes of the sandpile are illustrated below.

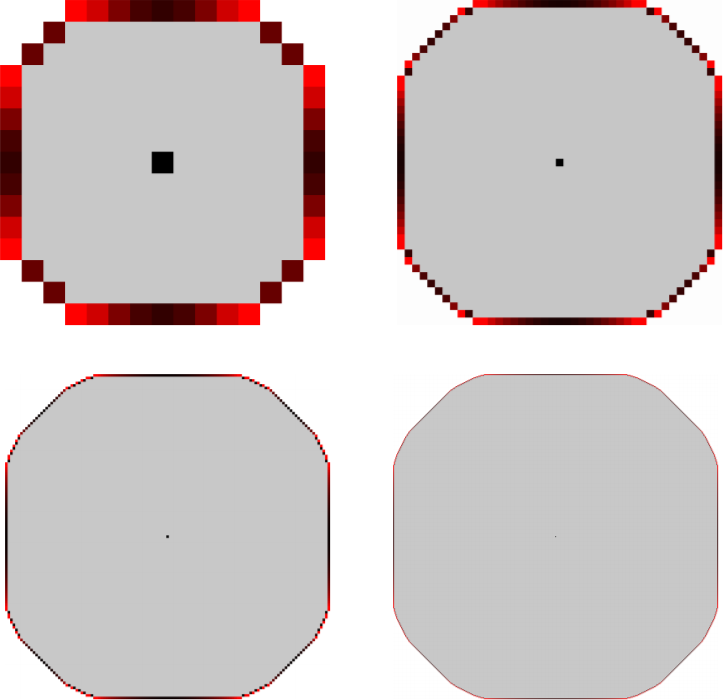
Absorbing part of the topplings into linear operators acting on graphs, we show that the model reaches a stable state in finitely many steps. We also prove that the final set of visited sites is the smallest domain (with respect to inclusions) in $\mathbb{Z}^d$ where the process can stabilize itself. The analysis is carried out in terms of a special function $u$, called the odometer, which is defined on $\mathbb{Z}^d$ and for each $x\in \mathbb{Z}^d$, $u(x)$ shows the total mass emitted from $x$ during the entire life-time of the process. We show a uniform (with respect to initial mass $n$) Lipschitz estimate on the odometer function, which (in part) implies Lipschitz regularity of the free boundary of the sandpile.

The underlying ideas of the analysis are largely motivated by potential theory, free boundary problems, and elliptic PDEs, building on top of these their combinatorial and probabilistic (random walk) counterparts. Our methods of this paper had already shown to be useful in other situations too. For instance, combined with the Least Action Principle for sandpiles proved by Fey, Levine, and Peres, the techniques developed for boundary sandpile enabled us to show for the first time, that the boundary of the scaling limit of the classical Abelian sandpile model with a single source, is Lipschitz regular in dimensions $d\geq 2$. To prove this, we show that the Least Action Principle combined with the discrete variant (considered in our paper) of the celebrated moving plane method of A.D. Aleksandrov, implies monotonicity of the discrete odometer function of the sandpile with respect to special directions determined by mirror symmetries of the unit cube of $\mathbb{R}^d$. We then observe, that this monotonicity of the odometer is being transferred to the scaling limit of the model, the existence of which was established only recently by Pegden and Smart. Relying on directional monotonicity of the odometer function, we show that at each point of the free boundary of the scaling limit, there are $d$-linearly independent directions along which the odometer of the Abelian sandpile is monotone. The latter allows us to show that at each point of the free boundary there is a double-cone (of uniform size) with the vertex at that point such that the free boundary remains entirely outside the interior of the cone. That condition implies Lipschitz regularity.

We close the paper with some open problems.

$K$-surface in $\mathbb{R}^{d+1} $ ($d\geq 2$) is a smooth, compact hypersurface of constant Gauss curvature equal to $K\geq 0$. A well-known problem in differential geometry and geometric analysis concerns description of possible boundaries of $K$-surfaces. Precisely, what conditions one has to impose on a collection $\gamma = \{ \gamma_1, ..., \gamma_n \}$ of disjoint ($d - 1$)-dimensional closed smooth embedded submanifolds, in order to guarantee an existence of a $K$-surface in $\mathbb{R}^{d+1}$ (in general immersed) having $\gamma$ as its boundary ? In particular, S.-T. Yau in his famous list of open problems asks (Problem N26) for conditions on a space curve $\gamma \subset \mathbb{R}^3$ to be the image of the boundary of an isometric embedding of the given smooth metric with positive curvature on the disk. In their analytic formulation, locally these problems mostly reduce to equations of Monge-Ampère type. Moreover, for the case of positive curvature $K>0$, the analysis is restricted to the case of elliptic equations, which then drives the study to the class of locally strictly convex hypersurfaces. With this in mind, an immediate necessary condition on $\gamma$ to bound a locally strictly convex hypersurface, is that its second fundamental form must be everywhere non-degenerate (in particular, in $\mathbb{R}^3$ this means that the curve $\gamma$ is free of inflection points). This elementary limitation, however, is not sufficient. It was shown by Rosenberg that there are further topological objections on $\gamma$, which was later demonstrated by Gluck and Pan to be not sufficient either. Most recently, Ghomi, answering a question of H. Rosenberg from 1993, proved that the torsion of any closed space curve bounding a simply connected locally convex surface vanishes at least 4 times. This important result is the only new necessary condition for the existence of $K$-surfaces since the condition obtained by Rosenberg in early 90's involving the self-linking number of the curve. There are a series of remarkable results on existence of $K$-surfaces by Caffarelli, Nirenberg, and Spruck (1984), Hoffman, Rosenberg, and Spruck (1992), Ghomi (2001), Trudinger and Wang (2002), and other. One of the results by Guan and Spruck (1993), which is particularly striking, proves an existence of embedded $K$-surfaces of arbitrary positive genus! This shows that the structure of these surfaces can be rather complicated, in spite of the strict restriction on the curvature.

For many years these problems have served as an important bridge between differential geometry and the analysis of partial differential equations, in particular for equations of Monge-Ampère type, where the advance on either side motivated and lead to new discoveries on the other end. Inspired by these developments, in this paper we introduce and study a class of $K$-surfaces with free boundaries. Namely, instead of prescribing a set $\gamma$ of closed smooth strictly convex codimension 2 submanifolds, and asking for a (locally) convex smooth manifold spanning $\gamma$, we treat the given $\gamma$ as part of the boundary of the sought-for surface. Then, fixing a smooth embedded submanifold $\gamma$ of codimension 1, we ask if there is a $K$-surface spanning $\gamma$ and hitting the (given) target manifold $T_0$ at some prescribed constant angle. In this generality, the problem seems to be out of reach, i.e. existence, uniqueness and regularity of solutions, as well as regularity and geometric properties of associated free boundaries. Our methods are of both geometric and analytic nature, drawing ideas from convex geometry, theory of Monge-Ampère equations, and free boundary problems. The free boundary (hitting angle) condition is the most delicate part of our analysis, where we introduce a special type of extension of solutions, which we named in the paper as Blaschke extension.

In periodic homogenization of Dirichlet problem for divergence type elliptic systems with oscillating Dirichlet data, one is faced with the difficulty of determining the limiting Dirichlet condition corresponding to the effective problem. This issue has been addressed very recently by Gérard-Varet and Masmoudi where it was shown that this limiting data depends on all ingredients involved in the problem, although without explicit characterization of the dependence. A more refined description of this data was given by Prange.

However, it is not known, if one starts with a problem where all the ingredients are smooth, can the boundary data corresponding to the effective problem develop singularities at the end of the homogenization process? The main objective of the current paper is to initiate the study of the regularity of this data, since it can shed a new light into the homogenization process, and one direct consequence would be the understanding of the regularity of homogenized solutions at the boundary.

In this paper we prove Lipschitz continuity of this limiting data on the boundary of the domain away from some lower dimensional set for layered media. One peculiar outcome of the main result of the paper is that for first order laminates, i.e. when the coefficient tensor in $\mathbb{R}^d$ depends only on 1 variable, the homogenized boundary condition has a unique extension to the entire boundary which is everywhere continuous except possibly two points on the boundary.

The starting point of the proofs are some of the main results in the above-mentioned papers, where in the first one it was shown that the homogenized boundary data is determined by certain ergodic constants (determined at each point of the boundary), called boundary layer tails, and which encode the averaging information for a given space direction. In the second one, C. Prange proved a representation formula for these constants, using which the present paper analyses the continuity properties of the boundary layer tails with respect to normal field of the boundary of the domain. The techniques used in the paper are of Fourier analysis, elliptic regularity theory, and linear algebra. We also discuss a closely related problem here, which turn out to have, somewhat surprisingly, a topological flavor.

This article is motivated by our papers treating homogenization of Dirichlet problem, the classical paper by Phong and Stein, and a recent interest in PDE problems involving rough boundaries, in particular the paper by Kenig and Prange. For a real-valued function $\psi \in C^\infty(\mathbb{R}^n)$ having bounded derivatives of all orders, consider the hypersurface $\Gamma = \{ (y, \psi(y)) \in \mathbb{R}^{n+1}: \ y \in \mathbb{R}^n \} $. For $f\in L^2(\mathbb{\mathbb{R}^n})$, $ \lambda>0$, and $(x, x_{n+1} ) \in \mathbb{R}^n \times \mathbb{R}$ define $$ T_\lambda f (x, x_{n+1}) = \int_\Gamma e^{i \lambda x\cdot y} \varphi_0((x,x_{n+1}),y ) K(x-y, x_{n+1}-y_{n+1}) f(y ) d\sigma(y,y_{n+1}) , $$ where $d\sigma$ is the surface measure on $\Gamma$, $\varphi_0$ is a real-valued function from the class $C_0^\infty (\mathbb{R}^{n+1} \times \mathbb{R}^n )$, and $K$ is a singular kernel satisfying $K\in C^\infty(\mathbb{R^{n+1}} \setminus \{0\} )$ and $| \nabla^\alpha K(z) | \lesssim_\alpha \frac{|z|^m}{|z|^{n+|\alpha|}}$ with $0\leq m < n$ for all $z\in \mathbb{R}^{n+1}\setminus \{0\}$ and any multi-index $\alpha \in \mathbb{Z}^n_+$. Here we have $n\geq 1$ and do not assume that $m$ is necessarily an integer.

For each fixed $x_{n+1}$ we study $T_\lambda$ as an operator from $L^2(\mathbb{R}^{n})$ to $L^2(\mathbb{R}^{n})$ and prove decay estimates for its operator norm as $\lambda \to \infty$. A special attention is paid to obtaining precise bounds with respect to the smoothness norms of the hypersurface $\Gamma$, as that estimates are being used to analyse the behavior of the operator $T_\lambda$ under small perturbations of a given fixed surface $\Gamma$. The latter problem is motivated by PDE problems with rough boundaries, where, for instance, the boundary can be technically $C^\infty$ however oscillating rapidly (and hence having large smoothness norms). In that setting standard techniques by partial integration toward controlling operators of the form $T_\lambda$, become inefficient, in view of the high oscillations of the surface. The approach we propose here handles efficiently the effects coming from surface oscillations.

In a similar spirit, when we allow the surface to oscillate, we consider a certain maximal operator associated with operators of the form $T_\lambda$ which captures the effect of the oscillation of the surface. More precisely, for a family of hypersurfaces $\{\Gamma_\varepsilon\}_{0< \varepsilon\leq 1}$ (having a certain structure) we analyse the boundedness of the operator $ T_\lambda^\ast f(x, x_{n+1}) = \sup\limits_{0< \varepsilon \leq 1} | T_\lambda^\varepsilon f(x,x_{n+1} ) |$, where $ (x,x_{n+1} ) \in \mathbb{R}^{n+1} $ and $T_\lambda^\varepsilon$ is defined as above but for the surface $\Gamma_\varepsilon$. Here the small parameter $0< \varepsilon \leq 1$ is meant to model an oscillatory behavior of the given family of hypersurfaces.

The second part of the paper studies operators of the form $T_\lambda$ where instead of the linear phase $x\cdot y$ we consider a fractional-type nonlinearity in the form of $|x-y|^\gamma$ with real $\gamma \geq 1$. This special choice of the phase function is partially motivated by PDE problems, in particular by the Helmholtz operator, and requires a completely new approach. We then apply our analysis to eigenvalue problem for the Helmholtz equation in $\mathbb{R}^3$ with some special source terms, and establish a decay estimate for solutions satisfying Sommerfeld radiation condition, as the eigenvalue tends to infinity.

The paper is essentially self-contained, and the proofs are based, among other things, on various decomposition arguments.

The paper concerns quantitative theory of periodic homogenization of divergence-type elliptic operators. Several papers in the literature address the question of convergence rate of homogenization in various settings, providing in particular how fast the process of homogenization holds. However, results treating to which extent homogenization can decelerate, provided it holds at the first place of course, are extremely scarce. The purpose of the present paper is to introduce a new method and develop some tools which will enable us to measure how slowly the homogenization can actually be in divergence-type setting.

In order to measure the speed of the process, we consider the following class of functions: call $\omega:[0,\infty)\mapsto (0,\infty)$ a modulus of continuity if it is continuous, one-to-one, and decreasing to 0 as $t\to \infty$. Now let $A= (A^{\alpha \beta}(x))_{\alpha, \beta=1}^d : X\mapsto \mathbb{R}^{d\times d} $ be a matrix-function defined on some domain $X\subset \mathbb{R}^d$ $(d\geq 2)$ where all elements of $A$ are bounded $C^\infty$ functions and the matrix $A$ is strictly elliptic on $X$. For a function $g\in C^\infty( \mathbb{T}^d )$ and a bounded subdomain $D\subset X$ with $C^\infty$ boundary, consider the following problem $$ (1) \ \ \ \ \ \ \ \ \ \ -\nabla \cdot A(x) \nabla u_\varepsilon (x) = 0 \text{ in } D \text{ and } u_\varepsilon = g(x/ \varepsilon) \text{ on } \partial D, $$ where $\varepsilon>0$ is a small parameter. Along with (1) consider also the homogenized problem $$ (2) \ \ \ \ -\nabla \cdot A(x) \nabla u_0 (x) = 0 \text{ in } D \text{ and } u_0 = \int_{\mathbb{T}^d} g(y) dy \text{ on } \partial D. $$

We prove the following result.

Theorem: *Let $A$ and $X$ be as above, and let $\omega $ be any modulus of continuity. Then there exist bounded, non-empty convex domains $D\subset X$ and $D_0 \subset D$ with $C^\infty$ boundaries, and a real-valued function $g\in C^\infty( \mathbb{T}^d )$ such that if $u_\varepsilon$ is the solution to (1) for $\varepsilon>0$, and $u_0$ to that of (2), then for some sequence of positive numbers $\{\varepsilon_k\}_{k=1}^\infty$ strictly decreasing to 0, one has the following:* $$ \qquad \qquad |u_{\varepsilon_k} (x) - u_{0}(x)| \geq \omega(1/{\varepsilon_k}), \ \forall x \in D_0, \ k = 1, 2, ..., $$ $$ |u_{\varepsilon}(x) - u_0(x)| \rightarrow 0 \text{ as } \varepsilon \rightarrow 0, \ \forall x \in D. $$

The proof of this result is constructive. The convex domain $D$ in question (which is not strictly convex of course) is being constructed having a flat piece on the boundary and otherwise having non-vanishing Gauss curvature. The existence of such convex domains with infinitely smooth boundary follows from Ghomi's construction. Departing from integral representation of solutions to (1) via Poisson kernel, we then split the integral in two parts, namely over the flat and non-flat portions of the boundary. We show, relying in part on the methods developed in our earlier papers, that the integral over non-flat portion has some prescribed decay rate determined by the embedding of $\partial D$ into $\mathbb{R}^d$ and independent of the rotation of the domain $D$. This part relies on the analysis of oscillatory integrals.

Next, we show that rotating $D$ we can put the flat portion of its boundary in such position that makes convergence of integrals over flat boundary as slowly as one wishes. For that we show that having a family of integrable functions with mild non-degeneracy requirements and growth control, one may construct a hyperplane and a smooth periodic function, such that restrictions of the functions of the family on the hyperplane integrated against periodically oscillating smooth function converge to their average over the hyperplane slower (uniformly for the entire family) than any given rate in advance. Here the normal direction of the hyperplane is constructed so that it is sufficiently badly approximated by rational directions. While the smooth periodic function in question is chosen with extremely sparse Fourier spectrum.

This constructive method we introduce in the paper, is also applied to boundary layer systems set in halfspaces (which were introduced by Gérard-Varet and Masmoudi and play a key role in homogenization of divergence type elliptic systems). There we show that depending on the position of the hyperplane convergence of solutions to their boundary layer tails far away from the boundary of the hyperplane can be as slowly as one wishes.

It seems plausible, perhaps with extra work, that the methods developed here should apply to Neumann problem or to almost-periodic setting too, or other similar settings.

The problem studied in this paper is similar to the one studies in our first paper in the series, however, here we are solely concerned with $L^p$ estimates. For $\varepsilon>0 $ let $ u_\varepsilon $ be the solution to the following Dirichlet problem $$ -\nabla \cdot A_\varepsilon(x) \nabla u_\varepsilon (x) =0 \text{ in } D \ \ \text{ and } \ \ u_\varepsilon(x) = g(x,x/ \varepsilon) \text{ on } \partial D, $$ where $D \subset \mathbb{R}^d $ $ (d\geq 2) $ is a bounded domain, $g(x, \cdot)$ is $ \mathbb{Z}^d $-periodic for any $ x\in \partial D$ and the operator is uniformly elliptic. We study the problem under strict convexity of the domain $D$ and smoothness of the data involved in the problem. Our results here are twofold. First, in the case when the coefficients $A_\varepsilon(x)$ do not depend on $ \varepsilon>0 $ (i.e. for some fixed $A$ we have $ A_\varepsilon \equiv A $, which means that the operator is fixed, but not necessarily constant) then for any $ 1\leq p < \infty $ we have the following convergence result $$ \tag{1} \qquad \|u_\varepsilon - u_0\|_{L^p(D)} \leq C_p \begin{cases} \varepsilon^{1/2p} ,& d=2 , \\ (\varepsilon |\ln \varepsilon |)^{1/ p}, & d=3 , \\ \varepsilon^{1/ p} , & d \geq 4, \end{cases} $$ where $ u_0 $ satisfies the same elliptic system but with Dirichlet data set to $ \overline{g}(x):= \int_{\mathbb{T}^d} g(x, y) dy $, where $ \mathbb{T}^d $ is the unit torus of $\mathbb{R}^d $. By establishing a certain type of ergodic theorem for scaled surfaces (which essentially states that large scalings of a strictly convex smooth surface modulo $\mathbb{Z}^d$ become equidistributed in $\mathbb{T}^d$ when the size of the scaling tends to infinity) we also show that the convergence rates given in $(1)$ are (generically) sharp in dimensions higher than three, and is sharp up to logarithmic factor in dimension three.

Second, when $ A_\varepsilon(x) \equiv A(x/ \varepsilon) $ for some $ \mathbb{Z}^d $-periodic tensor $A$, (the case of simultaneous oscillations in the operator and the boundary data) combining our method with a recent result by Kenig, Lin, and Shen we prove in dimensions greater than two and for some special class of coefficients $A$, that $$ \tag{2} \qquad \|u_\varepsilon - u_0\|_{L^p(D)} \leq C_p [ \varepsilon (\ln(1/ \varepsilon))^2 ]^{1/ p }, $$ for any $ 1\leq p< \infty $. In this special case our result settles the homogenization in its optimal form. Here $u_0 $ solves the homogenized problem with constant coefficient system and boundary data (which in our special case can be computed explicitly!) depending both on coefficients of the original as well as homogenized operators, the original boundary data, and the normal field of the boundary of the domain.

The motivation for revisiting the $L^p$-estimates obtained in the first paper of the series as a corollary to pointwise bounds, comes from the following: for the problem with simultaneously oscillating operator and boundary data, as in estimate $(2)$ above, the well-known paper by Gérard-Varet and Masmoudi proves that for dimension $d\geq 2$ one has homogenization of the $\varepsilon$-problem with convergence rate in $L^2$ of order $\varepsilon^{ (d-1)/(3d+5) -\delta } $ with arbitrary small loss $\delta>0$. Comparing this result with our $L^2$-estimate from [4], in the case of constant coefficient operators when the settings of both papers coincide, we see that the convergence exponent $1/4$, which was due to [4], gives a better convergence rate than $\frac{d-1}{3d+5} $ in dimensions up to $8$, and becomes worse for $d\geq 10$. This fact served as the motivating factor for us to revised the problem and look for optimal exponents of the convergence.

The proof of $(1)$, as in [4], is based on the analysis of singular oscillatory integrals. The reason, we are able to get better estimates here, is, very roughly, due to the fact that here we are dealing with domain integration (as opposed to pointwise estimates of [4]), where the singularity of type $ |x|^{-\alpha} $ (stemming from the Poisson kernel) near the origin has a better threshold for integration.

The refined analysis of this paper gives optimal bounds in $L^p$ however does not provide any pointwise estimates.

In the previous two papers of the series we studied the homogenization problem when the domain in question was strictly convex, i.e. when the boundary was "curved" in all directions. This paper studies the other extreme, when the boundary of the domain consists of flat pieces. More precisely, we let $D\subset \mathbb{R}^d$ $(d\geq 2)$ be a bounded and convex polygonal domain, i.e. a bounded convex domain which is an intersection of finite number of halfspaces. Then for a $\mathbb{Z}^d$-periodic function $g$ and strictly elliptic matrix \(A\) we study homogenization of the following Dirichlet problem $$-\nabla \cdot A(x) \nabla u_\varepsilon (x) =0 \text{ in } D \ \ \text{ and } \ \ u_\varepsilon(x) = g(x/ \varepsilon) \text{ on } \partial D,$$ where $\varepsilon>0$ is a small parameter. The analysis is carried out under a certain Diophantine condition on the normal vectors of the bounding halfspaces of $D$. Namely, if $\nu \in \mathbb{R}^d$ is the normal vector of arbitrary facet of $D$, then we assume that there are constants $C, \tau>0$ such that $$ |\nu \cdot m | > \frac{C}{|| m ||^\tau}, \qquad \text{for all } m\in \mathbb{Z}^d \setminus \{0\} .$$ It is well-known and is easy to see that for any $\tau> d-1$ almost all vectors are Diophantine (i.e. satisfy the above condition) with some constant $C>0$, so the polygon is in a general position. Then, under some regularity assumptions on $A$ and $g$ we prove homogenization results for the aforementioned problem, in the form of pointwise and $L^p$-estimates, where $1\leq p< \infty$. We also discuss the sharpness of the obtained $L^p$ convergence rates depending on the geometry of the domain.

The departing point in the proofs is the integral representation of solutions via the Poisson kernel. However, due to the radical change of the geometry of the domain, proofs are quite different and difficulties lie in totally different aspects. To see how the number-theoretical condition on normals is being utilized, observe that in integral representation of solutions, through the Poisson kernel, one is lead to study quantities of the form $\int_\Pi g( y/ \varepsilon ) d\sigma(y)$, where $\Pi$ is some nice subset of a facet of $D$. Now due to the periodicity of $g$, taking $\varepsilon \to 0$ amounts to considering $\frac{1}{\varepsilon} \Pi$ modulo $\mathbb{Z}^d$. Thus, in order to preserve the ergodicity of the system, i.e. being able to recover the entire information on $g$ from the slices $\frac{1}{\varepsilon} \Pi \mod \mathbb{Z}^d$, we need $\frac{1}{\varepsilon} \Pi$ to foliate the unit cell of periodicity of $g$ as $\varepsilon \to 0$. For the foliation it is enough to have irrationality of the normal direction of the facet of $D$ containing $\Pi$, and the Diophantine condition allows one to get quantitative control over this foliations, which are needed for effective estimates for the homogenization problem. The technicalities here are handled easily using Fourier analysis.

A significant portion of the paper is devoted to establishing a certain Hölder regularity for the Poisson kernel. Here the difficulties are introduced by the corners of the polygon, where the boundary is not regular. Since the Poisson kernel is the co-normal derivative of the Green's kernel, it suffices to understand the behavior of the Green's kernel in this corners. The high-level idealogy here stems from the fact that non-negative harmonic functions in cone-like domains (with the vertex at the origin) and vanishing on the boundary, have growth controlled by the first eigenvalue of the Laplace-Beltrami operator of the surface obtained as the intersection of the cone with the unit sphere (see this paper by Ancona). With this in mind we use freezing coefficient techniques and a certain type of Phragmen-Lindelöf argument to estimate the decay of the Green's kernel in the corners. Arguing by contradiction, if the Green's kernel doesn't have the decay rate in the corners dictated by the opening of the corner, after suitable blow-ups we generate a cone, and a positive harmonic function inside it having 0 Dirichlet data on the boundary, and with a certain estimate on its growth at infinity. By comparing this harmonic function with some two-dimensional barriers (built via the bounding hyperplanes of the cone) we arrive at a contradiction, since the growth becomes less than was expected. In the course of this comparison it is important to rule out cylindrical directions of the cone, so that the cone will have a single vertex. This is being achieved by homogeneity properties of harmonic functions in NTA-conical domains (see this paper by Kuran). These results on the regularity of kernels may be of independent interest.

It should also be remarked that here our analysis is bound to scalar equations and not systems as opposed to [4] or [5].

For a small parameter $ \varepsilon>0 $ let $ u_\varepsilon $ be the solution of the following elliptic system with a Dirichlet boundary condition $$ -\nabla \cdot A(x) \nabla u_\varepsilon (x) =0 \text{ in } D \ \ \text{ and } \ \ u_\varepsilon(x) = g(x/ \varepsilon) \text{ on } \partial D, $$ where $ D \subset \mathbb{R}^d $ $ (d\geq 2) $ is a bounded domain, $g$ is $ \mathbb{Z}^d $-periodic, and the operator is uniformly elliptic. Let also $ u_0 $ be the solution to the same elliptic system in $D$ but with Dirichlet data equal to the average of $g$ over its unit cell of periodicity. The main result of the paper states that under strict convexity of the domain $D$, and smoothness of the data involved in the problem, for any $ \kappa>0 $ one has the following pointwise bound $$ | u_\varepsilon(x) - u_0(x) | \leq C_\kappa \min\left\{ 1, \frac{\varepsilon^{(d-1)/2}}{(d(x))^{d-1+\kappa} } \right\}, \qquad \forall x\in D, $$ where $ d(x) $ denotes the distance of $ x $ from the boundary of $D$, and the constant $ C_\kappa =C(\kappa, d, A, D,g)>0 $. As a corollary to the pointwise bound, for any $ 1\leq p< \infty $ and any $ \kappa>0 $ we easily obtain $$ || u_\varepsilon - u_0 ||_{L^p(D)} \leq C_\kappa \varepsilon^{ \frac{1}{2p} - \kappa}. $$

The proofs are based on the analysis of singular oscillatory integrals, which enter the discussion through Poisson representation of solutions. There are two competing quantities in this representation; namely, the singularity of the Poisson kernel, and the oscillation of the boundary data. The smoothness of $A$ and $ \partial D $ allows us to obtain a nice (quantitative) control over singularities of the representation kernel and its derivatives. Next, the periodicity and smoothness of the boundary data $ g $, along with the strict convexity of the domain (which ensures non-zero Gauss curvature everywhere on the boundary) provide a lot of cancellations in the integral representing the solutions. One then does a careful trade-off between singularity of the integration kernel, and decay of the integral of the boundary data to get the desired estimate.

It is worthwhile to remark, that with some modification, the proposed approach leads to homogenization when instead of strict convexity of the domain, one requires that at each point of the boundary at least $1\leq m \leq d-1$ of the principal curvatures are non-vanishing (strict convexity corresponds to the case when $ m=d-1 $ ). The pointwise estimate in this case wll be similar, with $ d-1 $ in the exponent replaced by $m$, while the $L^p$-estimates will remain the same.

The paper explores various types of convergence for the greedy algorithm (i.e. when the Fourier series is rearranged according to decreasing order of the magnitudes of its coefficients) with respect to 1-dimensional renormalized trigonometric system. Necessary and sufficient conditions are found for system’s normalization to guarantee almost everywhere convergence, and convergence in $L^p(\mathbb{T}) $ for $ 1 < p < \infty $ of this approximation algorithm, where $ \mathbb{T} = \mathbb{R}/ \mathbb{Z} $ is the 1-dimensional torus. It is also proved that one cannot renormalize the trigonometric system so that to guarantee convergence almost everywhere of the approximation for all functions from $ L^1(\mathbb{T}) $, or uniform convergence for all continuous functions on the 1-dimensional torus. The proofs partially rely on the properties of some special trigonometric polynomials, such us Rudin-Shapiro sequence, Vallue-Poussin kernels, or Kheladze's polynomials. Along the results specific for the trigonometric system, we also give a sufficient condition on the weight sequence which ensures convergence of the weighted greedy algorithm with respect to any normalized basis in a general Banach space.