A diagram about funcoids and reloids
OpenYear of origin: 2018
Posted online: 2018-12-01 20:31:26Z by Victor Lvovich Porton
Cite as: P-181201.2
This is a previous version of the post. You can go to the current version.
Problem's Description
Define for posets with order $\sqsubseteq$:
- $\Phi_{\ast} f = \lambda b \in \mathfrak{B}: \bigcup \{ x \in \mathfrak{A} \mid f x \sqsubseteq b \}$;
- $\Phi^{\ast} f = \lambda b \in \mathfrak{A}: \bigcap \{ x \in \mathfrak{B} \mid f x \sqsupseteq b \}$.
Note that the above is a generalization of monotone Galois connections (with $\max$ and $\min$ replaced with suprema and infima).
Then we have the following diagram:
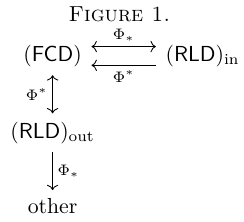
What is at the node "other" in the diagram is unknown.
Conjecture "Other" is $\lambda f\in\mathsf{FCD}: \top$.
Question What repeated applying of $\Phi_{\ast}$ and $\Phi^{\ast}$ to "other" leads to? Particularly, does repeated applying $\Phi_{\ast}$ and/or $\Phi^{\ast}$ to the node "other" lead to finite or infinite sets?
It seems that the node "other" is not $ \lambda f\in\mathsf{FCD}: \top $.
I conjecture $ \langle \Phi_{\ast} (\mathsf{RLD})_{\operatorname{out}} \rangle f = (\mathsf{FCD}) f $ where $ f $ is the reloid defined by the cofinite filter on $ A \times B $ and thus $ \langle (\mathsf{FCD}) f \rangle \{ x \} = \bot $ for all singletons $ \{ x \} $ and $ \langle (\mathsf{FCD}) f \rangle p = \top $ for every nontrivial atomic filter $ p $.
No solutions added yet